2021年11月8日
松本和夫『復刊 数理論理学』
共立出版,2001年
評者:角田 健太郎
1 はじめに
本書を評する前に、この分野に馴染みのない方のために、論理学(logic)あるいは数理論理学(mathematical logic)がどのような学問分野であるかを紹介する。
我々は日常生活の中で「〇〇さんの話からはその結論は出てこない(あるいは出てくる)」とか「××さんの話からは矛盾が出てくるから、××さんの話は成り立たない」と言うことがある。また、学問的研究の中では例えば、自然数論の公理から「$3$以上の$n$について、どんな数$x,y,z$をとってきても$x^n+y^n\neq z^n$」という定理が導かれるか否かが論じられる。我々が日頃行う“特定の諸前提からある結論を導き出す”という論証活動あるいは証明活動には、その帰結関係を特徴づける何らかの基準があることが窺える。ではその基準とはどのようなものだろうか。また、その基準を満たす論証は一般にどういった性質を持つだろうか。論理学はこうした問いを究明し、論証の在り様を探求する学問分野である。
しかしこのように言うと、まるで雲を掴むような話に聞こえるかもしれない。そこで、より具体的に、論理学は論証というものをどのようなものと捉え、そしてそれに対してどのようなアプローチによって研究を行うかのあらましを述べておこう。
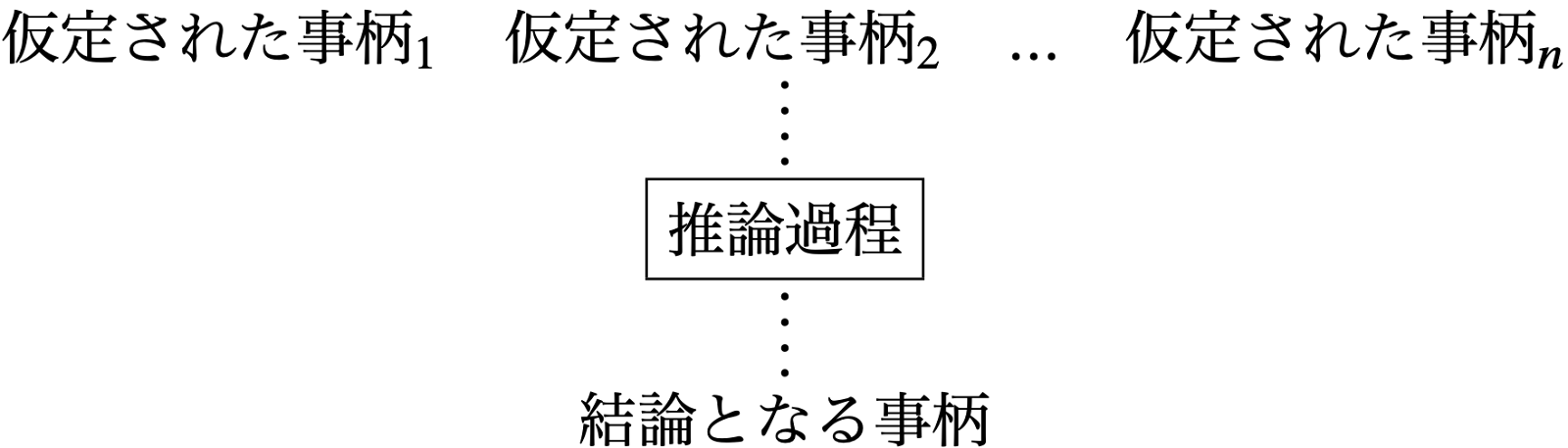
まず論理学のターゲットである論証(argument)あるいは証明(proof)とは、改めて述べ直すと「いくつかの仮定された事柄から、一定の推論過程を経て、ひとつの結論となる事柄を導き出すこと」である。論証のイメージは次のようなものである。
「仮定された事柄」や導き出された「結論となる事柄」に現れる“事柄”の表現を、論理学では命題(proposition)と呼ぶ。論証は命題を基本的構成要素として組み立てられていると考える。
さらに、“かつ”と“または”と“ならば”と“…でない”という四つの文結合子(connective)を用いることにより、命題を互いに結合させ新たな複合的な命題を作ることができると考える。$\phi$と$\psi$がそれぞれ命題であるとする。このとき、「$\phi$ かつ $\psi$」、「$\phi$ または $\psi$」、「$\phi$ ならば $\psi$」、「$\phi$ でない」という命題たちを作ることができる。例えば、「$12$は偶数である」という命題と「$12$は$3$の倍数である」という命題を文結合子“かつ”を用いて結合して「$12$は偶数でありかつ$12$は$3$の倍数である」という複合的な命題を作ることができる。そしてさらにこの命題と「$12$は$6$の倍数である」という命題を文結合子“ならば”を用いて結合して、「$12$は偶数でありかつ$12$は$3$の倍数であるならば、$12$は$6$の倍数である」というより複合的な命題を作ることができる。ここでひとつのポイントは、こうして作られた複合的な命題はどれも、それを作るために最後に用いられた文結合子(主結合子(main connective)と呼ぶ)が一つ決まるということである。命題「$12$は偶数でありかつ$12$は$3$の倍数である」の主結合子は“かつ”であり、命題「$12$は偶数でありかつ$12$は$3$の倍数であるならば、$12$は$6$の倍数である」の主結合子は“ならば”である。
さて、この主結合子に着目することにより、命題は互いの間で、あるものからあるものを推論することができると考える。そしてこれは先の四つの文結合子のそれぞれに定められた導入や除去の操作によってなされると考える。例えば、命題「$2$は素数である」と命題「$2$は偶数である」に対して、そこに文結合子“かつ”を導入して、命題「$2$は素数でありかつ$2$は偶数である」を推論することができる。また今度は反対に、例えば命題「$10$は$5$の倍数でありかつ$10$は$2$の倍数である」に対して、そこから“かつ”を除去して、命題「$10$は$5$の倍数である」を推論することができると考える。もちろん、命題「$10$は$5$の倍数でありかつ$10$は$2$の倍数である」に対して、そこから“かつ”を除去して、もう一方の命題「$10$は$2$の倍数である」を推論することもできる(文結合子“かつ”の除去の仕方には二種類あるわけである)。さらに文結合子“ならば”についての例を挙げると、命題「$123123123$の各位の数の和が$3$の倍数であるならば$123123123$は$3$の倍数である」と命題「$123123123$の各位の数の和は$3$の倍数である」に対して、そこから“ならば”を除去して、命題「$123123123$は$3$の倍数である」を推論することができる。“ならば”の導入による推論もあるのだが、やや複雑なので、ここでは触れるに留めておく。“または”と“…でない”についても、それらと対応する導入・除去操作による推論がある。なお、これら四つの文結合子が―初歩的な論証においては―十分であること、およびそれぞれに定められた導入・除去の仕方は、偶然的・恣意的なものではなく、代数的根拠が与えられるということをここで言い添えておく(ちなみに後で述べるように、『復刊 数理論理学』の第7章ではこの話題が扱われている)。
さて、これまで$\fbox{推論過程}$と言って指していた「諸仮定から結論を導き出す過程」とは、結合子の導入・除去操作の繰り返し適用だと考える。論証(特に正しい論証)とは、「仮定された諸命題から出発して、それらに対し、各結合子ごとに定められた導入・除去操作を一歩一歩繰り返し適用することで、結論となる命題を得ること」だと考えるのである。ある結合子についての導入・除去操作の1ステップのことを推論(inference)と呼び、そしてこれを定めたものを推論規則(inference rule)と呼ぶ。論証のイメージの一つの具体例が次のものである。
図において$\clubsuit,\clubsuit',\clubsuit''$で指した命題はそれぞれ仮定された命題を表し、$\spadesuit$で示した命題は結論となる命題を表している。$☆,☆',☆''$で示した箇所はそれぞれ1ステップの推論を表している。$☆$で示した箇所は、水平線の上の「$\mbox{命題}_1$」と「$\mbox{命題}_2$」という二つの命題に対して“かつ”の導入規則が適用され水平線の下の「$\mbox{命題}_1\mbox{かつ}\mbox{命題}_2$」という命題が得られたことを表している。$☆'$で示した箇所は、水平線の上の「$\mbox{命題}_1\mbox{かつ}\mbox{命題}_2$」と「$(\mbox{命題}_1\mbox{かつ}\mbox{命題}_2)\mbox{ならば}(\mbox{命題}_3\mbox{かつ}\mbox{命題}_4)$」という二つの命題に対して“ならば”の除去規則が適用され水平線の下の「$\mbox{命題}_3\mbox{かつ}\mbox{命題}_4$」という命題が得られたことを表している。$☆''$で示した箇所は、水平線の上の「$\mbox{命題}_3\mbox{かつ}\mbox{命題}_4$」という命題に対して“かつ”の除去規則が適用され水平線の下の「$\mbox{命題}_3$」という命題が得られたことを表している。上のように論証が組み立てられるということを以て、三つの仮定「$\mbox{命題}_1$」,「$\mbox{命題}_2$」,「$(\mbox{命題}_1\mbox{かつ}\mbox{命題}_2)\mbox{ならば}(\mbox{命題}_3\mbox{かつ}\mbox{命題}_4)$」から結論「$\mbox{命題}_3$」が帰結することが示された、と考えるのである。以上が論理学が捉える論証の大まかな姿である。
さて、論理学の一つの目的は、この論証というものを過不足なく明示的に表現する記号体系を整備・開発することである。このような目的で作られた記号体系は論理体系(logical system)と呼ばれる。ひとつの論理体系は、まずどのような記号表現が意味のある合法的な表現であるかを定め、そしてさらにそれらに対してどのような推論規則を適用してよいかを定めることで決定される。ひとつの論理体系は、典型的には次のような諸定義によって定められる。
- 命題を表現する論理式(formula)と呼ばれる記号列の定義
- 推論規則を表現する推論図(inference figure)と呼ばれる図式の定義
- これはまさに先の論証のイメージで用いた水平線を用いて、論理式を図式的に配置する方法を定めることによってなされる。
- 論証を表現する証明図(proof figure)と呼ばれる図式の定義
- これは推論図を木構造状に連鎖させる仕方を定めることによってなされる。
ある論理式がある論理体系で定まる証明図の結論であるとき、その論理式はその論理体系で証明可能(provable)であるという。
論理学はこの論理体系という道具立てを主軸として論証の在り様を研究する。例えば、何らかの特徴を満たす事柄(すなわち内容)を表現する命題の集合はどのような論理体系で証明可能な論理式の集合と一致するかという問い(およびその反対の問い)や、定義を異にする二つの論理体系の間に同等な関係や部分の関係があるかという問いなどが研究課題となる。前者のような、命題が表現する内容と論理体系の間の関係を扱う論理学の研究部門は意味論(semantics)と呼ばれ、他方後者のような、命題が表現する内容には踏み込まずに命題の言語的構造に則して―つまり命題の内容ではなく、その言語表現の側面を利用することによって―命題間の推論連関を明らかにする論理学の研究部門は証明論(proof theory)と呼ばれる。
さて、松本和夫著の『復刊 数理論理学』(以下、本書)には、以上であらましを述べた論理学研究の実際が定義・定理・証明の進行の形で精確に書かれている。扱われているのは、主に20世紀に解明された論理学の諸結果、特に証明論部門における諸結果である。
以下では本書の主な特徴をより詳しく述べる。
さて先ほど、論理体系の形式化を考える際の推論の捉え方として、文結合子の導入・除去によって推論の進展を捉える考え方を見た。実は、この形式化手法はひとつの代表的なものであり、自然演繹(natural deduction)と呼ばれる。この自然演繹を含め、論理体系の形式化手法として代表的なものには、
- ヒルベルト系(Hilbert system)
- 自然演繹(natural deduction)
- シーケント計算(sequent calculus)
の三つがある。なお、ヒルベルト系はFregeによって開発され、HilbertとRussellによって整備された。また自然演繹とシーケント計算は、Hilbertの門下生のGentzenによって開発された。これらはその定義の仕方によって、意味論的性質の証明のしやすさと証明論的性質の証明のしやすさに関して多少の相違を持っているのだが、本書ではこれら三手法それぞれを学ぶことができる。そして本書では、特に三番目のシーケント計算に関する証明論的話題が非常に豊かに盛り込まれている。証明図が実は計算の対象であるという事実を、シーケント計算の体系上で成り立つカット除去定理の証明を通して具体的に学ぶことができるのが本書の最大の特徴である。
ところで、論理体系の形式化手法という区別とはまた別の区別として、論理の違い、すなわち論理体系で証明可能な論理式の範囲の違いによる論理体系の区別がある。代表的なものとして、古典論理(classical logic)と直観主義論理(intuitionistic logic)という二つの論理がある。大まかには、古典論理はどの命題も真か偽のいずれかの値を持つと意味論的に考えることができる論理であり、他方で直観主義論理は真偽いずれにも定まらない値を持つ命題を認める論理である。直観主義論理の論理体系で証明可能な論理式はすべて古典論理の論理体系で証明可能であるが逆は成り立たない。この意味で直観主義論理は古典論理よりも弱い論理であるが、一方で意味論的には直観主義論理の方が命題の意味内容として細かな内包的区別を持つことが知られている。そして何よりも重要であるのは―これは本書評の最後でも改めて述べるが―現在プログラミング言語理論の研究分野において中心的な役割を果たしているのは、自然演繹によって形式化された直観主義論理体系だという事実である。本書では自然演繹によって形式化された直観主義論理体系の証明論的議論も多く盛り込まれている。本書は、その発刊年からして、プログラミング言語理論との接続は強く意図されたものではないと考えられるが、結果として現在読む価値が非常に高い論理学書であると言える。
まとめると、論理体系には、その形式化手法の区別と論理の区別により以下のような諸体系があるのだが、
| 論理\形式化手法 | ヒルベルト系 | 自然演繹 | シーケント計算 |
|---|---|---|---|
| 古典論理 | $HK$ | $NK$ | $LK$ |
| 直観主義論理 | $HJ$ | $NJ$ | $LJ$ |
本書では特に$NJ$と$NK$および$LK$と$LJ$の部分に眼目が置かれている。シーケント計算を通して証明図の計算の具体像を学ぶことができ、そして自然演繹による直観主義論理体系を学ぶことができる本書は、論理とプログラムに跨る計算という現象を論理の視点から学ぶための足掛かりとなる書であると言える。
2 本書の構成と概要
本書の構成と概要、および読み進める当たっての評者による補足説明を以下で述べる。
本書は全7章からなっている。特に第3,4,5章が本書のメインとなる部分であり、ここで自然演繹とシーケント計算、そしてシーケント計算による自然数論の話題が扱われる。
大まかな内容を順に紹介する。まず第1,2章では、古典ヒルベルト系$HK$に関する意味論的・証明論的諸性質が扱われる。ここで、ひとつの論理体系に関する意味論的・証明論的研究の大まかなあり方を知ることができる。ただし、ヒルベルト系の証明図は自然演繹のものと比べると、それが表現する論証のイメージを得るのに独特の慣れを要求するものとなっていると評者には感じられる。意味論的研究と証明論的研究のいずれを行うにあたっても、まずは証明図が表現するところの論証が何であるかを身体に馴染ませることが必要であるが、ヒルベルト系の証明図はその道を険しいものにしてしまうと評者には思える。そうした理由で、第1,2章はあまり本腰を入れすぎず、後の第3章の自然演繹の学習によって証明図と論証の明確なイメージを得たあとで、再び戻ってくる計画で読むのがおすすめである(特に自然演繹はその名の通り、論証の自然な理解の仕方を教えてくれる形式化だと感じられる)。第3章以降は、証明論に特化した内容となっている。第3章では、直観主義自然演繹$NJ$と古典自然演繹$NK$が定義され、その間に成り立つ証明論的定理が示される。ここで、文結合子の導入と除去の操作のアイデアによる論証の形式化を豊富な具体例を通して学ぶことができる。第4章では、自然演繹を踏まえて開発されたシーケント計算の基本事項が扱われる。古典シーケント計算$LK$と直観主義シーケント計算$LJ$が定義され、それらの上で成り立つカット除去定理(cut elimination theorem)と呼ばれる定理が示される。これは証明論の核となる定理である。ここで、驚くべきことに、証明図は実は計算項を含んでいる(一種のプログラムのようになっている)という事実を知ることができる。本書には、証明図を計算する手順が細かく具体的に書かれている。第5章は、前章の$LK$にさらに自然数論の公理を追加し、今度は自然数論がどのような計算を含んでいるかが論じられる。自然数論の計算は$\varepsilon_0$という超限順序数に関わる計算を含んでいるという深淵な定理の証明の粗筋が解説される。第6章は、様相論理(modal logic)と呼ばれる、古典論理を拡張した論理のシーケント計算による形式化が扱われる。第7章は、各文結合子について定められた推論規則の形が何故その形であるかの代数的説明が論じられる。以上が本書の大まかな内容である。
以下ではより詳しく各章の内容を述べる。
第1章は、著者が序文で述べている通り、論理学の入門の章となっている。ただし繰り返しになるが、本章で扱われるヒルベルト系から論証(およびこれを踏まえた証明論と意味論の研究)に馴染むことは、言わば登山ルートとして険しいと評者には思われる。本章および次章は、一度ザッと読み、そして第3章の自然演繹で論証に馴染んだあとで、もう一度戻って読むのが吉であろう。さて、本章では意味論と証明論それぞれの基本となる考え方が書かれている。まずはじめに、命題として真/偽いずれかの内容を持つものが取り上げられる。そして、真理表という道具立てを用いることにより、“素材となる命題が真/偽のどの値をとろうとも常に真の値をとる”という特徴を持つ複合的命題のグループを考えることができる事が論じられる。このグループに属する命題はトートロジー(tautology)と呼ばれる。次いで、古典ヒルベルト系$HK$が定義され、$HK$の論証で要となる演繹定理と呼ばれる証明論的定理が示される。そして、$HK$で証明可能な論理式の集合が、トートロジーである命題の集合を過不足無く表現しているという事実、つまり「トートロジーである命題の集合」と「$HK$で証明可能な論理式の集合」とが一致するという意味論的定理が示される(「ある命題の集合」と「ある論理体系で証明可能な論理式の集合」が一致することは完全であると呼ばれ、そしてこの完全性を主張する定理は完全性定理と呼ばれる)。最後に本章では、この完全性の結果を用いて、$HK$の無矛盾性($HK$からはある論理式とその否定の両者が証明可能ではないという性質)と独立性($HK$の推論図が表現する推論のどれもについても、その推論図以外の推論図を組み合わせることよって表現することができないという性質)が示される。
第2章は、述語論理と呼ばれる論理を扱う章である。本書評ではこれまで、“かつ”と“または”と“ならば”と“…でない”という四つの文結合子に関わる論理を考えてきた。専らこれら文結合子の働きにのみ着目する論理は命題論理(propositional logic)と呼ばれる。述語論理(predicate logic)とはこの命題論理を拡張したものであり、命題が表現する事柄に“対象が満たす性質や関係”が新たに導入される。述語論理の論理体系では、例えば、「4の倍数はすべて偶数である」という仮定と「6の倍数はすべて3の倍数である」という仮定と「12は4の倍数でありかつ6の倍数である」という仮定から「偶数でありかつ3の倍数である数が存在する」という結論を導く論証を表現できる。なお、述語論理は数学の証明の枠組みとなる論理である。本書ではこれ以降、述語論理が扱われる。さて、第2章ではまず、第1章で定義した$HK$を述語論理へと拡張し、述語論理版の古典ヒルベルト系$HK$が定義される。次に、$HK$で証明可能な論理式の集合と一致するような命題の集合を特徴づけることを目標に、フレームやモデルと呼ばれる種々の道具立てが定義される。そして、それら道具立てによって定まる命題の集合と$HK$で証明可能な論理式の集合とが一致すること、すなわち述語論理版の完全性定理が示される。なお本書では、この完全性定理の証明はHenkinの定理を用いて証明される。Henkinの定理は集合論の公理であるZornの補題によって証明される。Zornの補題については、例えば[11]と[7]で知ることができる。
第3,4,5章は証明論に関する話題であり、直観主義自然演繹$NJ$と古典自然演繹$NK$、古典シーケント計算$LK$と直観主義シーケント計算$LJ$、そしてシーケント計算により形式化された自然数論がそれぞれ定義され、それらについて成り立つ証明論的定理の証明が扱われる。
第3章では、まずRussellのパラドクスとそれを受けて鮮明となった数学の哲学の立場のひとつである直観主義の思想および直観主義論理についての解説が書かれている。そして、直観主義自然演繹$NJ$と古典自然演繹$NK$が定義・解説される。次の図は$NJ$の証明図の一つの例である。
$\wedge,\supset,\lnot$はそれぞれ文結合子“かつ”、“ならば”、“…でない”を表している。$A,B,C$はそれぞれ文結合子を持たない命題を表している。$\bot$は矛盾命題を表している。ところで、本章には上のような$NJ,NK$の証明図が豊富に記載されており、これらを自分で書いて答え合わせができるようになっている。証明図を自分でたくさん書くことは、直観主義論理の論証がどのような論証活動であるかを理解する助けになると評者は実体験から思う。第1,2章の$HK$についても同様のことが言えるが、特に本章の直観主義論理について理解を得るためには、紙とペンを用意して“習うより慣れろ”の方針で読み進めるのがおすすめである。また自然演繹の証明図を完成させるコツは“図式を下から上に遡って書く”という書き方をすることである。さて本章では次いで、$NJ$と$NK$の関係に関する証明論的定理であるGlivenkoの定理が示される。この定理は、ある論理式が$NK$で証明可能であるとき、かつそのときに限って、その命題に文結合子“…でない”を二回施した論理式が$NJ$で証明可能であるということを主張する定理である。この定理の証明もまた自分で書いて追うことで、直観主義論理と古典論理の差異の理解、そして論理が異なるとはどういうことかについての理解が深まると評者は思う。第3章の最後は、Russellのパラドクスを受けて立てられたもう一つの数学の哲学の立場であるHilbertの形式主義およびその有限の立場と呼ばれる思想についての解説が書かれている。後の第5章で解説されるように、Gentzenはこの形式主義の立場のもとで自然数論の無矛盾性を証明するに至る―ただしGentzenによる証明が有限の立場に収まるものであるかについては議論の余地があり、この話題は[5]で読むことができる―のであるが、その証明の理解の準備としてここでは超限順序数が解説される。
第4章では、シーケント計算が扱われる。ここで本章の内容に入る前に、まずシーケント計算についての簡単な説明を評者の方で与えておく。シーケント計算の理解のために出発点となるのは自然演繹である。さて、自然演繹の証明図において推論規則によって結びつけられている論理式の現れのそれぞれは、その論理式を導くに至った仮定が何であるかの情報すなわち命題の帰結関係に関する情報を担っていると考えることができる。本書評冒頭の論証のイメージの例で対応する事柄を考えると、例えば、先の図の左側の2行目の「命題1かつ命題2」は、それが「命題1」と「命題2」の二つの仮定から帰結するという情報を担っていて、また右側の「(命題1かつ命題2)ならば(命題3かつ命題4)」は、それが「(命題1かつ命題2)ならば(命題3かつ命題4)」という仮定(すなわち自分自身)から帰結するという情報を担っていると言える。結論「命題3」は、それが「命題1」と「命題2」と「(命題1かつ命題2)ならば(命題3かつ命題4)」の三つの仮定から帰結するいう情報を担っていると言える。さてシーケント計算の証明図とは、大まかなイメージとしては、自然演繹の証明図の各論理式の現れの各々に、それを導くに至った仮定の情報を書き込んだものである。ただし、シーケント計算には自然演繹と大きく異なる点がある。それは、自然演繹の推論規則が文結合子の導入・除去操作によって定められていたのに対して、シーケント計算の推論規則(詳しくは推論規則のうちの文結合子に関する推論規則)は、“仮定されている論理式への文結合子の導入”および“結論されている論理式への文結合子の導入”という2種類の導入操作によって定められるという点である(すなわち、シーケント計算の文結合子に関する推論規則には導入規則しかない)。シーケント計算は、論証の進展を“仮定と結論の帰結関係の複雑化の過程”として表現するのである。論証の進展の捉え方のこの転換により、実は、シーケント計算によって定められた古典論理体系および直観主義論理体系は、それぞれが無矛盾であることを純粋に証明論的な議論すなわち証明図の言語表現的な構造に関わる議論のみで示すことができる(ヒルベルト系の無矛盾性が意味論的定理をバイパスすることで示されたことと対比されたい)。Gentzenによって示されたこの証明論的議論はカット除去定理(cut elimination theorem)と呼ばれる。さて本章では、シーケント計算による古典述語論理体系$LK$および直観主義述語論理体系$LJ$がまず定義される。次の図は$LK$の証明図の一つの例である。
$\frak{A}_1,\ldots,\frak{A}_m\rightarrow\frak{B}_1,\ldots,\frak{B}_n$という形の表現(ここで$\frak{A}_1,\ldots,\frak{A}_m$と$\frak{B}_1,\ldots,\frak{B}_n$はそれぞれ論理式の列を表している)は一つの帰結関係を表し、これがシーケント(sequent)と呼ばれる。一つのシーケントにおいて、矢印「$\rightarrow$」の左側の論理式の列$\frak{A}_1,\ldots,\frak{A}_m$は前件と呼ばれ、これを構成する論理式のそれぞれは仮定されている命題を表す。対して矢印「$\rightarrow$」の右側の論理式の列$\frak{B}_1,\ldots,\frak{B}_n$は後件と呼ばれ、これを構成する論理式のそれぞれは結論となる命題を表す。矢印「$\rightarrow$」の左側に現れるカンマ「$,$」は“かつ”の意味であり、矢印「$\rightarrow$」の右側に現れるそれは“または”の意味である。つまり一つのシーケント$\frak{A}_1,\ldots,\frak{A}_m\rightarrow\frak{B}_1,\ldots,\frak{B}_n$は“前件の命題が全て仮定されたとき、後件の命題の少なくとも一つが帰結する”ということを表している。上の図は「$\lnot\lnot D$が表す命題と$\lnot A\supset((C\supset(B\wedge C))\supset\lnot D)$が表す命題と$B$が表す命題が仮定されたとき、$A$が表す命題が―古典論理では―帰結する」という帰結関係を導く論証を表現しているわけである。さて、本章では$LK,LJ$両者についてのカット除去定理の証明がGentzenによるオリジナルの証明をほぼ忠実に再現する形で書かれている。論理学的事実の概要としては説明は以上で尽きるのであるが、評者が見るに、この定理の証明の具体像がとにかくおもしろい。ここで評者は、そのおもしろさを伝えられるようGentzenの証明の要点の説明を以下で試みてみようと思う。ひとまずGentzenのカット除去定理の大意を説明すると、それは、
論理的な回り道を含む正しい論証は、論理的な回り道を含まないものへと変形することができる
というものである。ここで「論理的な回り道」とは、一種の三段論法に相当する推論のことである。この推論を表現する推論図がシーケント計算の推論規則(詳しくは推論規則のうちの構造に関する推論規則)においてカット(cut)と呼ばれる。三段論法が論理的な回り道と呼ばれる所以は、次のような帰結関係に関する一種の三段論法
において命題$\chi$が、帰結関係「諸仮定${\phi_1,\ldots,\phi_m,\psi_1,\ldots,\psi_n}$から結論${\upsilon}$が帰結する」を直接導くことが難しい局面で、${\phi_1,\ldots,\phi_m,\psi_1,\ldots,\psi_n}$にも${\upsilon}$にも含まれていない(すなわち回り道となる)情報で論証の見通しを与える中間地点の役割を果たしていると捉えられることによる(八王子駅から池袋駅へ移動するとき、最短の直線距離で移動することを考えるよりも回り道である新宿駅を間に挟んだ方が移動の見通しがよくなることと類比的だと評者は考える)。Gentzenのカット除去定理は、与えられた論証がこの三段論法(論理的な回り道)をいくつ含んでいようとも、最終的に導かれている帰結関係を変えることなしに、論証の進展過程を変化させることによってそれら三段論法のすべてを取り除くことができる(すなわちどんな論証も、導かれている帰結関係の情報のみを使って回り道なしに論証を再構成することができる)ことを主張している。この論証の進展過程の変形に相当する証明図の変形のことがカット除去と呼ばれる。本章で示されているカット除去の手続きを見るとわかる通り、正しい論証は、驚くべきことに、三段論法を取り除く手続きに関する知恵の輪のようなパズル的構造を持っているのである。次の図は$LK$の証明図の一つの例に対するカット除去の実際の様子である。
下向き二重矢印「$\Downarrow$」のそれぞれは、カット除去手続きの1ステップの適用を表している。カット除去手続きが進むごとに、$cut$の水平線の左上にあるシーケントの後件の右端の論理式および$cut$の水平線の右上にあるシーケントの前件の左端の論理式がどんどん単純な形になっていくことが見て取れるだろう。ところでまた、もうひとつ興味深い話題がある。それは、三段論法によって導かれる帰結関係から消えてしまう命題(先の例で言うところの$\chi$)は、数学の証明における補題を表現したものとなっている―まさに証明の見通しを与えるものとなっている―と言えるのであるが、カット除去定理が成り立つという事実は、補題の有用性あるいは意味が、それを証明の変形によって滞りなく除去することができるという計算可能性と結びついているということを教えているということである。カット除去定理は、補題あるいは一般に定理の意味(そしてそこに現れる語の意味)が計算によって与えられるという一つの哲学的見方を与えていると見受けられるのである。以上が評者が興味深いと考えるところのGentzenのカット除去定理の要点の説明である。なお本章の最後では、カット除去定理の系として$LK,LJ$の無矛盾性が示せること、およびカット除去定理の応用として命題論理版の$LK,LJ$の決定問題(古典命題論理(直観主義命題論理)で成り立つ命題を表現する論理式のどれについてもそれを結論に持つ$LK$($LJ$)の証明図を構成する手続きが存在すること)、および$LJ$の選言文特性(ある選言文が$LJ$で証明可能であるとき、その選言肢のいずれかを導く$LJ$証明図が構成できること)、そして$LJ$において排中律(「$\phi$または($\phi$でない)」という命題)が証明可能でないことの証明が書かれている。
第5章では、カット除去の手法を応用したGentzenによる自然数論の無矛盾性証明の解説が書かれている。まずPeanoの公理と呼ばれる自然数論の公理が解説され、Peanoの公理によって加法関数が定義できることが示される。次に第4章で定義した$LK$にPeanoの公理を加えた記号体系を自然数論として定義し、そしてこの記号体系が無矛盾であることを示すためのGentzenのアイデアが説明される。そのアイデアとは、この記号体系では矛盾を表現するシーケントを導く証明図が構成されることはないということを、カット除去と同じ要領による証明図の変形によって示す、というものである。ただし、この記号体系にはPeanoの公理の数学的帰納法の推論図が含まれていることがポイントとなり、カット除去の手続きは、第4章の$LK,LJ$の場合と異なった振る舞いをし、第3章の最後で扱われた超限順序数にまで訴えなければその手続きが停止することを示せない、ということが解説される。なお本書には書かれていないが、このGentzenの自然数論の無矛盾性証明はGödelの不完全性定理の主張を裏付けるような結果となっている。この話題は[5]で読むことができる。
第5章までで、20世紀前半までの論理学の基本的結果に関する話題は一段落である。このあとの第6,7章は古典論理の拡張である様相論理と呼ばれる論理に関する話題と、代数系と論理に関する話題である。
第6章では、以上までで見てきた論理では扱われていなかった文結合子である「…は必然的である」および「…は可能である」の二つが古典論理に新たに加わった様相論理と呼ばれる論理に対する証明論的アプローチの入門的解説が書かれている。まず著者により、自然演繹を用いて様相概念を含む推論の具体像が示される。次に先行研究の中で発見されたいくつかの様相論理体系が紹介され、そしてこれらのシーケント計算による形式化が解説される。様相論理体系のカット除去定理の証明が与えられ、それぞれが無矛盾であることが証明される。本章の様相論理体系は主として命題論理に様相演算子を導入した論理の範囲での話題(すなわち様相命題論理の話題)であるが、様相述語論理についての話題としてBarcanの公理と呼ばれる論理式が$S5$と呼ばれる様相論理体系で証明可能であることが示されている。様相述語論理については[1]に詳しく書かれている。
第7章は、序文で著者が述べているように補章の役割を果たす章である。これまで見てきた直観主義論理や古典論理や様相論理が特定の束(すなわち順序集合の特別な場合)と概念上の対応関係を持っていることが解説される。具体的には、直観主義論理は相対擬捕束と、古典論理はBoole代数(可補分配束)と、様相論理S4は位相束と、という具合に対応している。ところで第3,4章において、古典論理と直観主義論理の差異は$NJ,NK$の記号体系上の差異、あるいは$LK,LJ$の記号体系上の差異として現れたが、本章では、その差異を代数構造の特徴として統一的に理解する視点が与えられている。なお[10]には、こうした束論の視点からGentzenのシーケント計算を得る議論が述べられている。
3 評者コメント
本書は20世紀の論理学の、特に証明論部門の基本的結果やその効用、そしてそのおもしろさを、無駄なく網羅的に精確に学ぶことができる書である。すでに上で述べた通り、本書には証明図が豊富に掲載されており、自分で書いて理解する論理学の学習法を自然に助けてくれる。評者は、論理学には自分で図式を書いてみないことにはわからないことがたくさんあるということをこの本に教わった。
また、類書の中でも本書は貴重な内容を多く含んでいる。Gentzenのカット除去定理は証明論の基本定理であるが、Gentzenのオリジナルの証明の全容を知ることができる書は、評者が知るところ和書ではほとんどこの本だけである。Gentzenの自然数論の無矛盾性証明についても同様である。また、第6章の様相論理体系のシーケント計算による形式化およびそのカット除去について詳しく書かれているのも和書としては珍しく、この内容が扱われているのは評者が知る限りはおそらく本書と[8]と[9]だけである。
網羅的に証明論の基本事項と考え方が扱われている本書であるが、しかし現在の証明論研究の状況からすると大きな欠落となってしまっているトピックがひとつあると評者には見受けられる。それは、情報科学分野と証明論の関係である。このトピックは、序文でほんの二三言触れられているが、本文では一切取り扱われていない。実は、本書の復刊前の最後の版が出版された1970年代から、証明論は情報科学のとりわけプログラミング言語理論と密接な関わりを持つことが次第に明らかとなったのである。より具体的には、本書で定義された直観主義論理体系$NJ$は、型付きラムダ計算(typed lambda calculus)と呼ばれる、関数型プログラミング言語のモデルである記号体系と対応していることが明らかとなったのである。詳しくは、$NJ$による論証の構成は、整合的なコンピュータプログラムを構築することと同一視できるのである。この対応はカリー・ハワード同型対応(Curry-Howard isomorphism)と呼ばれる。この発見により、例えば特定のコンピュータプログラムが破綻せずに動作することを、本書で扱われているような証明論における図式変形による無矛盾性証明の手法によって保証することができるようになった。証明論の情報科学的応用の道が開かれたのである。また反対に、論証をある種のプログラムだと見なす視点が与えられたことで、論証の結論となっている命題の意味を、プログラムの挙動すなわち特定の計算に関する振る舞いとして解釈する道具立てが得られた。命題やそこに出現する語の意味に関する新たな哲学的考察の道が開かれたのである。カリー・ハワード対応については、和書では[8]と[6]に入門的事項がまとめて書かれている。より詳しい事柄については[3]に書かれている。ちなみに以上は直観主義論理に関する話題であったが、古典論理体系$NK$についてのカリー・ハワード対応が明らかになったのは1990年代と比較的最近であり、古典シーケント計算$LK$に関するカリー・ハワード対応については明らかになったのは2000年代である。これらの発見については[2]、[4]に書かれている。
4 補遺
『復刊 数理論理学』は、復刊前の増補版の出版年がいまから50年前ということもあり、現在の数理論理学で標準的となっている用語とは異なる用語が一部採用されている。本書評では、できるかぎり現在標準的となっている用語を採用して解説を行った。『復刊 数理論理学』で採用されている用語と本書評で採用した用語の対応関係は次の通りである。
| 『復刊 数理論理学』 | 本書評 |
|---|---|
| 命題計算 | 命題論理の論理体系 |
| $H_p$ | 命題論理の古典ヒルベルト系$HK$ |
| 述語計算 | 述語論理の論理体系 |
| $H_q$ | 述語論理の古典ヒルベルト系$HK$ |
| sequential calculus | sequent calculus |
| 式 | シーケント |
謝辞
本書評の執筆にあたり、東京都立大学の岡本賢吾先生、山﨑紗紀子氏にたくさんの有益なアドバイスを賜りました。この場をお借りして感謝申し上げます。また、執筆の機会を与えてくださったTARB編集委員の皆様、並びに丁寧なコメントと有益なアドバイスを下さったTARB評議員の皆様にも、感謝申し上げます。
参考文献
- Fitting,M. and Mendelsohn,R.L. (1998) First-Order Modal Logic, Synthese Library, 277, Springer
- Griffin,T. (1990) A Formulae-as-Types Notion of Control. 17'th symposium on Principles of Programming Languages (POPL'90), pp.47–58
- Sørensen,M.H. and Urzyczyn,P. (2006) Lectures on the Curry–Howard isomorphism, Studies in Logic and the Foundations of Mathematics, 149, Elsevier
- Wadler,P. (2003) Call-by-value is dual to call-by-name. Proceedings of the eighth ACM SIGPLAN International Conference on Functional Programming (ICFP’03), pp.189–201
- 安東祐希 (2010) ゲンツェンの論理学-基本定理と無矛盾性証明- 『法政哲学』 第6号 pp.i–xiv
- 飯田隆(編・著)、津留竜馬、吉満昭宏、遠山茂朗、 岩本敦、三平正明、照井一成、峯島宏次 (2005) 『知の教科書 論理の哲学』 講談社選書メチエ 講談社
- 内田伏一 (1986) 『集合と位相』 数学シリーズ 裳華房
- 小野寛晰 (1994) 『情報科学における論理』 情報数学セミナー 日本評論社
- 菊池誠(編・著)、佐野勝彦、倉橋太志、薄葉季路、黒川英徳 (2016) 『数学における証明と真理 : 様相論理と数学基礎論』 共立出版
- 前原昭二 (2010(初版1966、復刊2010)) 『復刊 数理論理学序説』 共立出版
- 松坂和夫 (1968) 『集合・位相入門』 岩波書店
出版元公式ウェブサイト
共立出版
https://www.kyoritsu-pub.co.jp/bookdetail/9784320016828
評者情報
角田 健太郎(つのだ けんたろう)
現在、東京都立大学人文科学研究科博士課程在籍。主な論文は「なぜ古典論理に計算的意味を与えるのか ― SLCにもとづくDummett的観点の拡張の試み ― 」(『新進研究者 Research Notes』第3号、2020年)。専門は論理学の哲学。